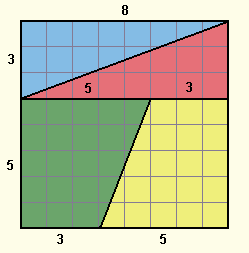
Παίρνουμε ένα τετράγωνο χαρτόνι και το διαγραμμίζουμε σε οκτώ επί οκτώ ίσα μικρότερα τετράγωνα, σαν σκακιέρα. Στη συνέχεια κόβουμε το χαρτόνι πάνω στις γραμμές που φαίνονται στο πρώτο σχήμα.
Αναδιατάσσουμε τα κομμάτια ώστε να σχηματίσουμε ένα νέο σχήμα που είναι ένα ορθογώνιο παραλληλόγραμμο με διαστάσεις 13 x 5, όπως φαίνεται στο δεύτερο σχήμα.
Το αρχικό τετράγωνο αποτελούνταν από 8 x 8 = 64 μικρότερα τετράγωνα, ενώ το νέο σχήμα αποτελείται από 13 x 5 = 65 τετράγωνα. Πως προέκυψε αυτό το επιπλέον τετραγωνάκι;



1 σχόλιο:
Λύση :
Η απάντηση σε αυτό το φαινομενικό παράδοξο είναι πως τα κομμάτια που αναδιατάσσουμε για να φτιάξουμε το ορθογώνιο δεν εφάπτονται ακριβώς μεταξύ τους κατά μήκος της μεγάλης διαγωνίου. Μένει ανάμεσά τους ένας κενός χώρος ο οποίος φαίνεται με καφέ χρώμα στο παρακάτω σχήμα.
Σχήμα από την απάντηση της ιστοσελίδας μου
Πιο συγκεκριμένα, αν τοποθετήσουμε το γαλάζιο και το κίτρινο κομμάτι ώστε να σχηματίζουν μεταξύ τους ορθή γωνία, η κλίση της πλευράς τους που κανονικά θα έπρεπε να εφάπτεται είναι διαφορετική. Αυτό φαίνεται από τις γωνίες φ και θ που σημειώνονται στο σχήμα. Έχουμε tanφ = 3/8 = 0,375 και tanθ = 2/5 = 0,4. Άρα οι δύο γωνίες δεν είναι μεταξύ τους ίσες. Το εμβαδόν του κενού χώρου που μένει ισούται με το εμβαδόν ενός μικρού τετραγώνου. Η παρακάτω ανάλυση αφορά τη γενίκευση αυτής της εφαρμογής.
Το ίδιο φαινόμενο θα παρατηρούταν και στην περίπτωση που κόβαμε με τον ίδιο τρόπο ένα χαρτόνι με διαστάσεις 13 x 13 και το αναδιατάσσαμε σε ένα ορθογώνιο 21 x 8. Τώρα όμως το αρχικό τετράγωνο έχει 169 τετραγωνάκια ενώ το νέο ορθογώνιο έχει 168. Δηλαδή στην περίπτωση αυτή λείπει αντί να περισσεύει ένα τετράγωνο. Αυτό γεωμετρικά οφείλεται στο ότι τα κομμάτια του ορθογωνίου τώρα επικαλύπτονται κατά μήκος της μεγάλης διαγωνίου.
Ας δούμε πως αναλύεται μαθηματικά κάθε περίπτωση αυτής της εφαρμογής. Πίσω της κρύβεται μια πολύ γνωστή ακολουθία στους μαθηματικούς με το όνομα ακολουθία Fibonacci. Κάθε όρος αυτής της ακολουθίας είναι το άθροισμα των δύο προηγούμενων όρων της, αρχίζοντας με τους όρους 0 και 1. Έτσι, οι πρώτοι όροι της ακολουθίας Fibonacci είναι οι: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Συμβολίζουμε με F(n) τον n-οστό όρο της ακολουθίας Fibonacci, αρχίζοντας την αρίθμηση από n=0. Έτσι π.χ. F(6) = 8. Το εμβαδόν του νέου σχήματος διαφέρει από το αρχικό πότε κατά -1 και πότε κατά +1 τετραγωνάκι, ανάλογα με το n. Αυτό μαθηματικά γράφεται ως:
F(n+1) x F(n-1) - F(n) x F(n) = (-1)^n
μια ισότητα που είναι γνωστή σαν ταυτότητα Cassini και η οποία αποδεικνύεται μαθηματικά.
Μόνο για μέλη: Γράψτε την απάντησή σας