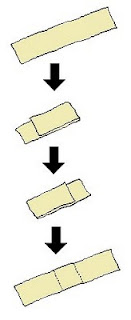
Ο Κωστάκης έχει πάνω στο γραφείο του μία λωρίδα χαρτιού και προσπαθεί να τη διπλώσει στη μέση. Σηκώνει το δεξί άκρο της, το τσακίζει σε κάποιο σημείο που του φάνηκε κεντρικό και το διπλώνει πάνω στο αριστερό άκρο. Βλέπει όμως πως από τα αριστερά περισσεύουν 10 εκατοστά χαρτιού. Ξανανοίγει το χαρτί και πιάνει το αριστερό άκρο το τσακίζει σε ένα διαφορετικό σημείο και το διπλώνει πάνω στο δεξί άκρο. Όμως πάλι περισσεύουν 10 εκατοστά, αυτή τη φορά από τη δεξιά πλευρά του χαρτιού. Απογοητευμένος απλώνει τη λωρίδα χαρτιού στο γραφείο του που τώρα έχει πάνω της τα ίχνη από δύο τσακίσεις. Πόσα εκατοστά απέχουν αυτές οι δύο τσακίσεις μεταξύ τους;
Μετρήστε την ευφυΐα σας!
Πόσο έξυπνοι είστε; Βρείτε την απάντηση σε αυτό το ερώτημα λύνοντας μερικούς από τους καλύτερους γρίφους αυτού του blog, συγκεντρωμένους σε μία εφαρμογή Android. Κατεβάστε την εφαρμογή από το Google Play Store.
Τετάρτη 3 Μαρτίου 2010
Εγγραφή σε:
Σχόλια ανάρτησης (Atom)

3 σχόλια:
Λύση :
Απέχουν 10 εκατοστά.
Μετά τις διπλώσεις, η λωρίδα έχει χωρισθεί σε τρία τμήματα. Τα δύο ακριανά είναι ίσα λόγω συμμετρίας και ονομάζουμε το μήκος τους a, ενώ το μεσαίο τμήμα που είναι το ζητούμενο το ονομάζουμε x. Όταν το χαρτί είναι διπλωμένο περισσεύουν από τη μία πλευρά του 10 εκατοστά. Αυτό μπορεί να γραφεί σαν εξίσωση ως:
a + x = a + 10
από την οποία προκύπτει πως x = 10.
(είναι ίσα λόγω συμμετρίας)
ΤΙ ΠΑ ΝΑ ΠΕΙ ΑΥΤΟ????!!!
ΕΤΣΙ ΣΤΟ ΑΚΥΡΟ???!!!
ΒΑΛΕ ΚΑΙ ΜΙΑ ΥΠΟΤΥΠΩΔΗ ΑΠΟΔΕΙΞΗ!!!!!
@Skeptikalisthw: Μην τσαντίζεσαι. Είναι ίσα λόγω συμμετρίας σημαίνει πως αν το ένα από τα δύο ήταν μεγαλύτερο τότε κατά την τσάκιση θα απείχε λιγότερο από το άλλο από την άκρη του χαρτιού.
Μόνο για μέλη: Γράψτε την απάντησή σας